- Have any questions?
- +44 785 307 7576
- help@sciqics.com
Chemometrics
How can Chemometrics help you?

What is Chemometrics?
Chemometrics is the chemical discipline that uses mathematical, statistical, and other techniques to design or select optimal measurement procedures and experiments, and to provide maximum relevant chemical information by analyzing chemical data.
The chemometrics approach uses multivariate methods, i.e., all variables are considered at the same time to build a data driven model to characterise a physical system. It is mainly used to understand the patterns of association in the data set and increase the experimental dynamic measurement ranges of methods such as spectroscopy.
Using chemometrics to improve instrument capabilities
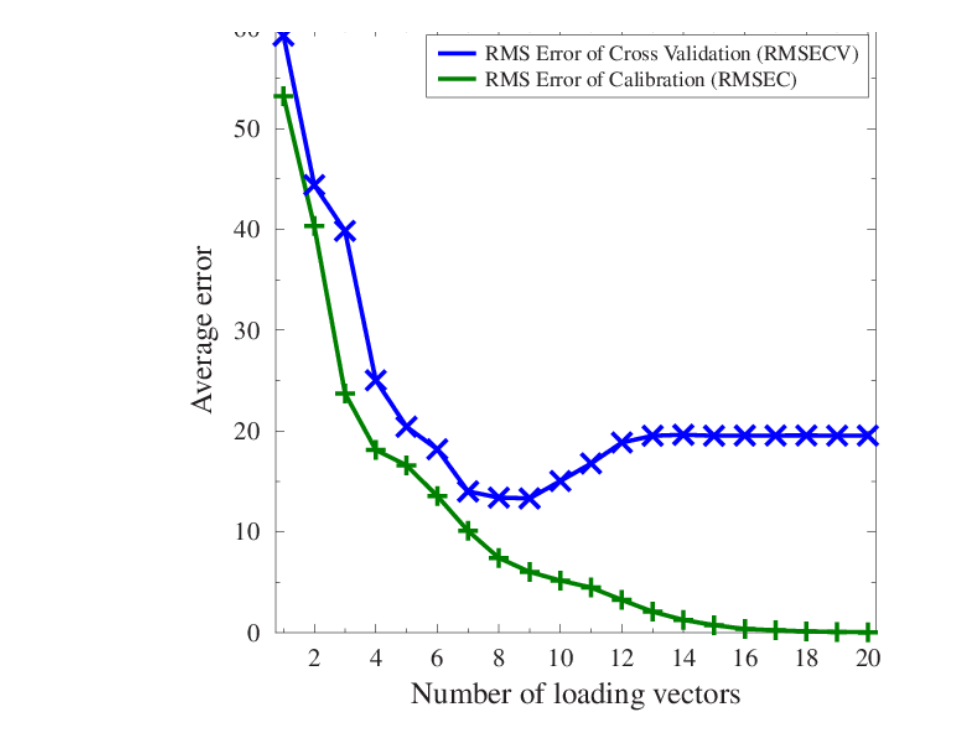
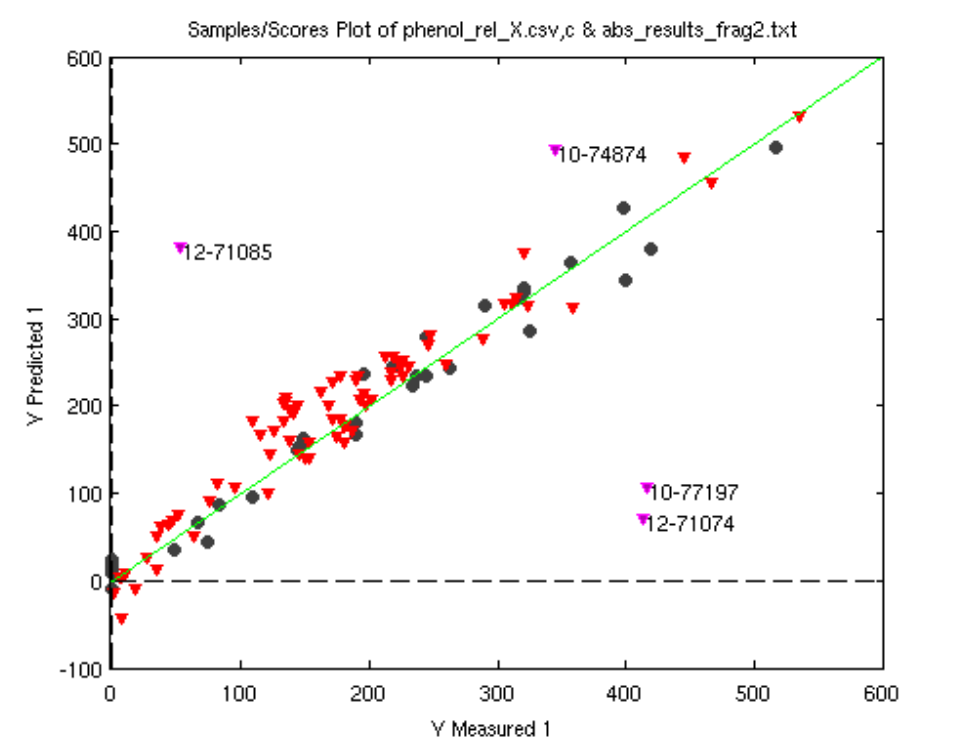
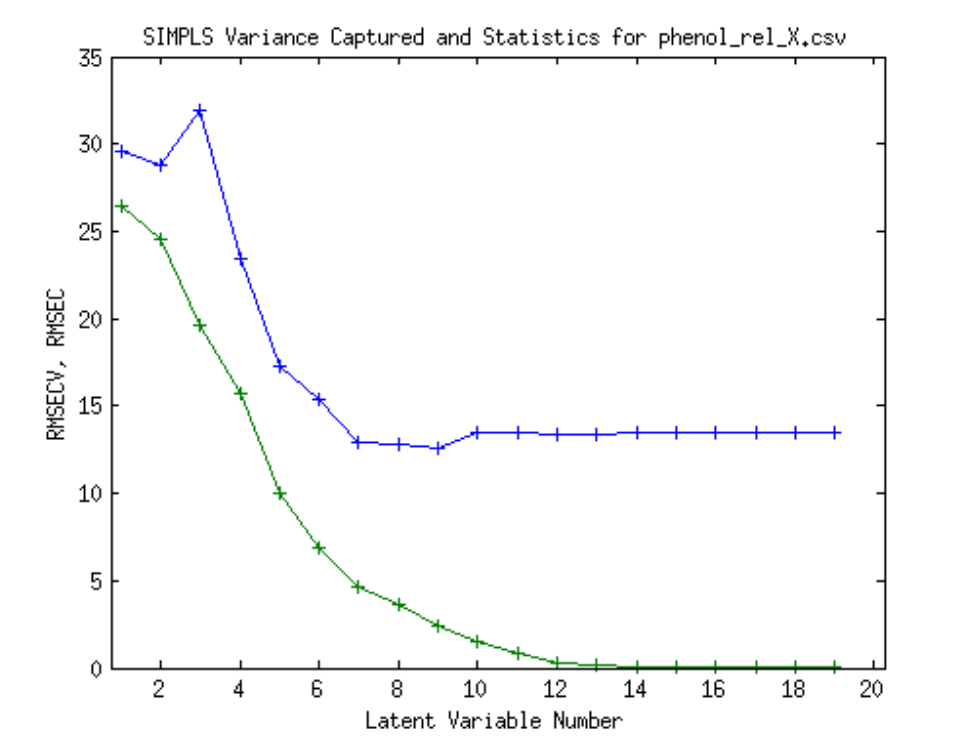
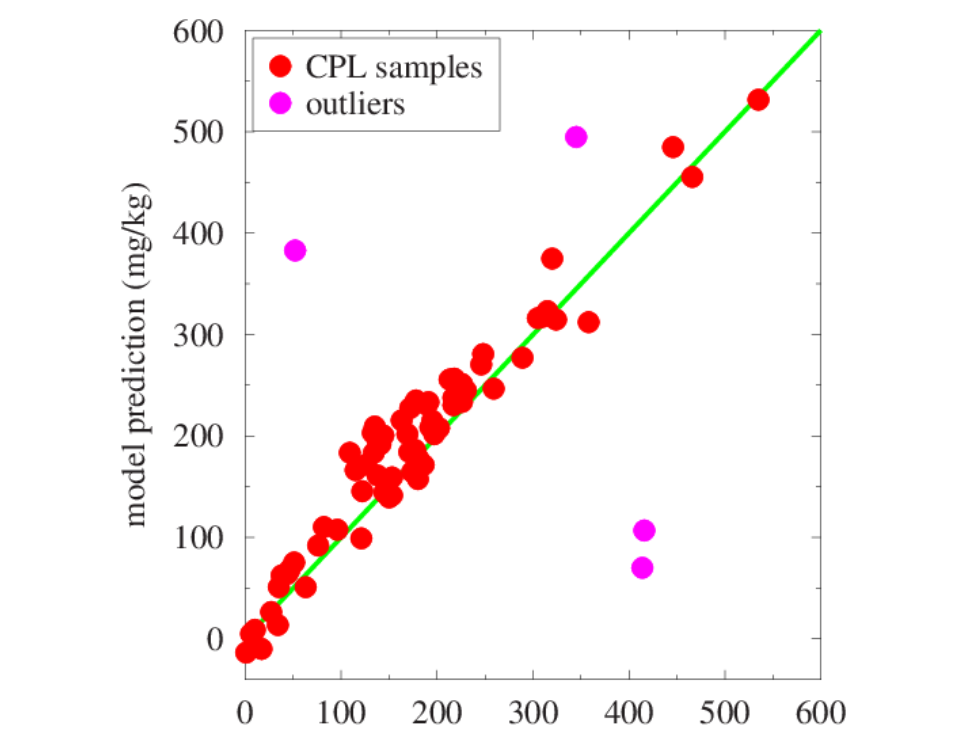
Many chemical processes and applications of chemometrics involve calibration. The objective is to develop models which can be used to predict properties of interest based on measured properties of the chemical system such as flow, temperature, infrared and mass spectra.
For instance in spectroscopy, data is collated from a number of samples, including concentrations for an analyte of interest for each sample (the reference) and the corresponding infrared spectrum of that sample. Multivariate calibration techniques such as partial-least squares (PLS), or principal component (PCR) can then used to construct a mathematical model that relates the multivariate response (spectrum) to the concentration of the analyte of interest. This model can be used to predict the concentrations of new samples at much lower concentrations than that which can be conventionally determined from the spectra.

What can we do for you?
We can help you develop a deeper understanding and elucidation of your data sets and processes by designing experiments, preprocessing data for analysis and developing suitable chemometric models. These models will help us derive meaningful and actionable information and discern the variables which have physical relevance and avoid data artefacts.
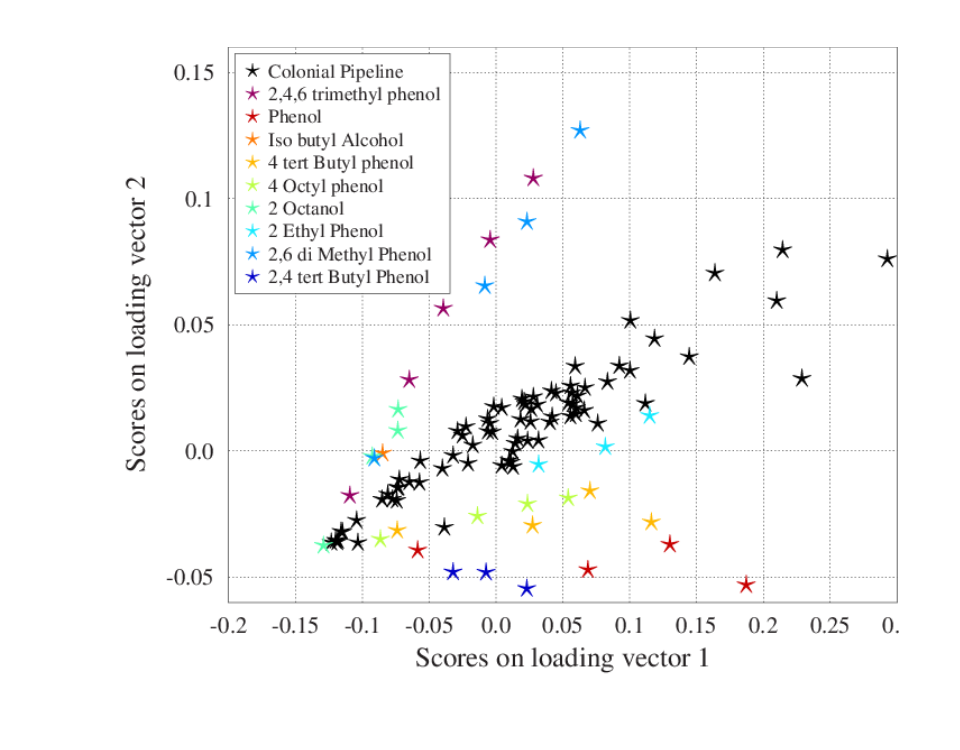
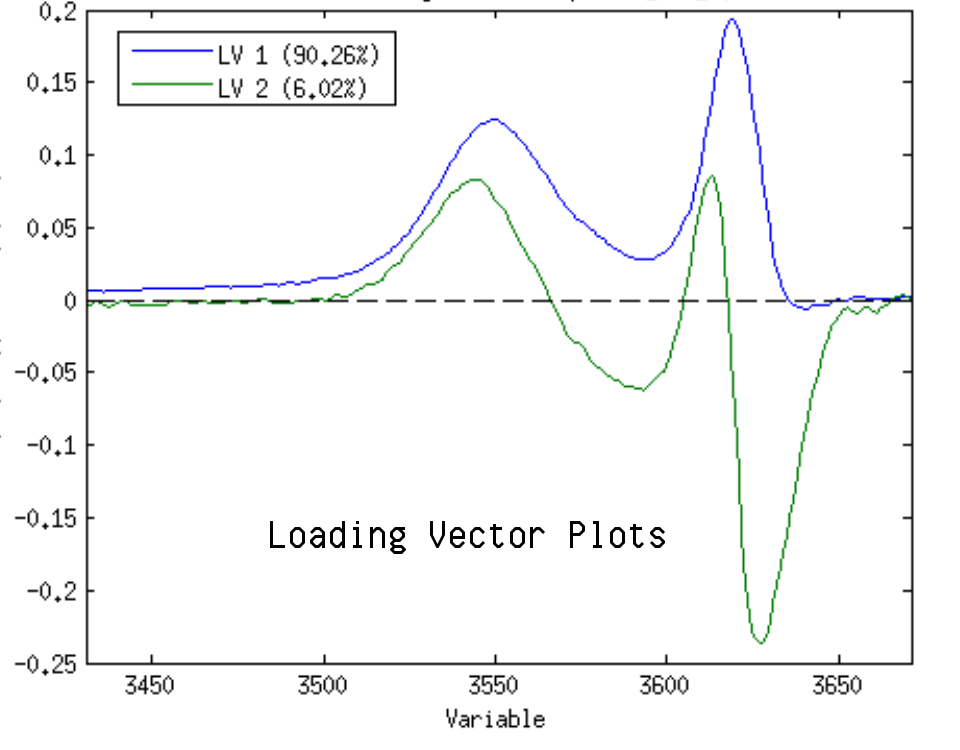
Although datasets such as infrared spectra maybe highly multivariate, they also have a strong and often linear low-rank structure. This makes them suitable for analysis using techniques such as principal components analysis (PCA) and partial least-squares (PLS). The central idea of PCA is to reduce the dimensionality of a data set consisting of large amounts of interrelated variables, yet keeping maximum variation in the data set. Unsupervised classification (also termed cluster analysis) is also commonly used to discover patterns in complex data sets, and again many of the core techniques used in chemometrics are common to other fields such as machine learning and statistical learning.